


Next: Priors and proposals
Up: Bayesian phylogenetics
Previous: Bayes' theorem
Contents
Computing the denominator of
equation 2.5
is infeasible for realistic sized problems. A Markov Chain
Monte-Carlo method is therefore used. The standard
Metropolis-Hastings MCMC algorithm can construct a Markov chain in
our state space 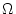 by iterating a two step
process (Hastings, 1970; Metropolis et al., 1953). Firstly, a new state
by iterating a two step
process (Hastings, 1970; Metropolis et al., 1953). Firstly, a new state 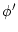 is drawn from the actual state
is drawn from the actual state 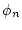 according to some proposal
mechanism. The proposed state is then accepted or rejected with some
probability which depends on the ratio of the posterior probabilities of the
two states
according to some proposal
mechanism. The proposed state is then accepted or rejected with some
probability which depends on the ratio of the posterior probabilities of the
two states 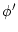 and
and 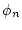 and of the proposal.
After a ``burnin'' period, the chain converges to an
equilibrium, under quite weak conditions. After discarding an
initial portion of the chain, states are distributed according to
the posterior probability density
and of the proposal.
After a ``burnin'' period, the chain converges to an
equilibrium, under quite weak conditions. After discarding an
initial portion of the chain, states are distributed according to
the posterior probability density 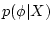 . PHASE
can produce a large
sample from the posterior
probability density and with this sample one can compute the posterior
probability of any identifiable phylogenetic feature of interest.
For instance the posterior probability of a specific topology is
simply given by the fraction of times this topology appears in our MCMC
sample. Similarly we can fit a posterior probability density curve to the
gamma distribution parameter.
. PHASE
can produce a large
sample from the posterior
probability density and with this sample one can compute the posterior
probability of any identifiable phylogenetic feature of interest.
For instance the posterior probability of a specific topology is
simply given by the fraction of times this topology appears in our MCMC
sample. Similarly we can fit a posterior probability density curve to the
gamma distribution parameter.



Next: Priors and proposals
Up: Bayesian phylogenetics
Previous: Bayes' theorem
Contents
Gowri-Shankar Vivek
2003-04-24