

Next: Markov chain Monte-Carlo (MCMC)
Up: Bayesian phylogenetics
Previous: Bayesian phylogenetics
Contents
A Bayesian approach to phylogeny reconstruction requires the
definition of a parameter space 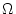 which contains the sets
of all possible combined states
which contains the sets
of all possible combined states
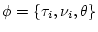 where the symbol
where the symbol 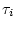 labels the
labels the 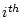 possible tree
topology,
possible tree
topology, 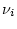 are the branch lengths associated with this
topology and
are the branch lengths associated with this
topology and 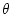 is a set of allowed parameters for our
evolutionary model (e.g.,
rate ratios
is a set of allowed parameters for our
evolutionary model (e.g.,
rate ratios
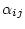 , nucleotide or base-pair frequencies
, nucleotide or base-pair frequencies 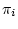 ,
gamma distribution parameter
,
gamma distribution parameter 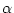 , ...). According to Bayes' theorem,
we can calculate the posterior probability of the combined state
, ...). According to Bayes' theorem,
we can calculate the posterior probability of the combined state
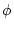 given sequence data
given sequence data 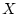 ,
,
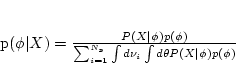 |
(5) |
where 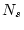 is the number of possible tree topologies for a data
set containing
is the number of possible tree topologies for a data
set containing 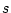 species,
species, 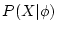 is the likelihood of the data
and
is the likelihood of the data
and 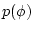 is the prior probability density
associated with state
is the prior probability density
associated with state 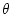 .
.
Gowri-Shankar Vivek
2003-04-24