Invariant and discrete gamma models

Substitution rates are definitely variable over sites of a sequence for many real dataset if not all. Including the heterogeneity of rates in substitution models is widely recognized as an important factor in the fitting to data. One attempt to take this acknowledged biological fact into account is to suppose that a proportion of sites are invariant while others evolve at the same single rate. PHASE provides this invariant model. One extra parameter in the model governs the proportion of sites with zero rate of evolution.

Models that allows continuous variability of mutation rates over sites are more realistic and the gamma model of Yang (1994) outperforms the invariant model. The discrete gamma model is implemented in PHASE . The continuous rate distribution is approximated with a discrete distribution which is computationaly tractable and sites are divided into $k$ equally probable rate categories. A single parameter $\alpha$ governs the shape of this distribution and the substitution rates for all categories. The mean $E(r)$ of the gamma distribution is the average mutation rate of our substitution model as stated earlier and its variance is $V(r)=E(r)^{2}/\alpha$. 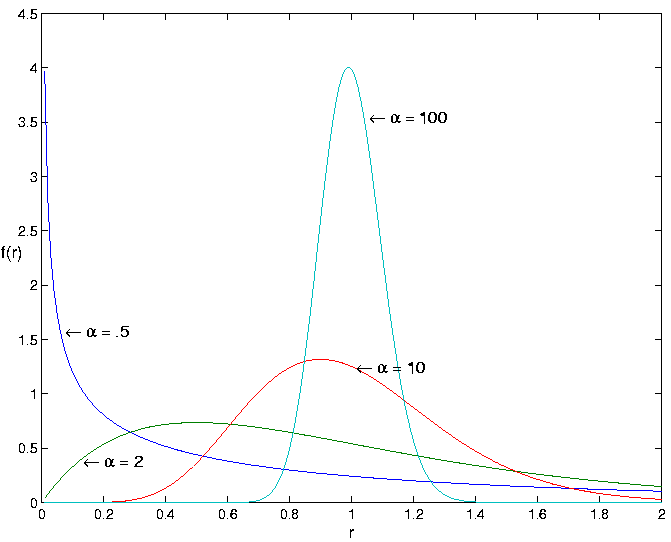A small alpha suggests that rates differ significantly between sites with few sites having high rates and others being practically invariant; on the contrary, large $\alpha$ models weak rate heterogeneity (see figure 2.6). When $\alpha \rightarrow +\infty$, the gamma model reduces to the single rate model. Computational requirement of the discrete gamma model is roughly linear, i.e., the application of a discrete gamma model with $k$ categories is about $k$ times slower than the use of a model where rate heterogeneity is not considered.

Figure 2.6: Probability density function of several gamma distributions of rate heterogeneity with mean $E(r)=1$